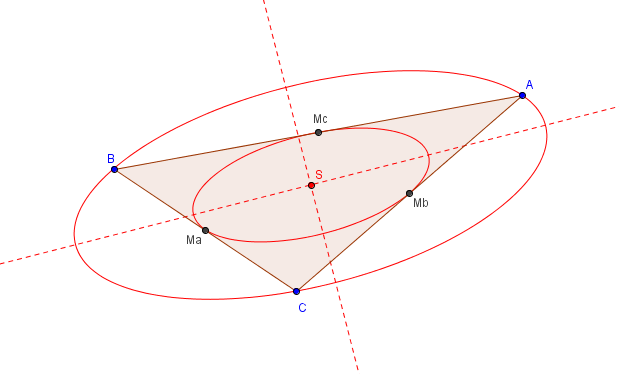
Steinerellipsen

Viele Ellipsen lassen sich an Dreiecken bilden. Besondere Ellipsen sind die Steinerellipsen. Die Inellipse tangiert die Seitenmitten des Dreiecks und hat als Mittelpunkt den Schwerpunkt des Dreiecks. Die Steinerinellipse hat den größt möglichen Flächeninhalte einer Ellipse im Dreieck. Auf der Umellipse liegen die Eckpunkte des Dreiecks. Der Mittelpunkt und die Achsen sind mit denen der Inellipse identisch. Der Flächeninhalt von Inellipse zu Umellipse hat das Verhältnis von 1:4. Die Hauptachse der Ellipsen ist eine Regressionsgerade für Punkte einer Streuellipse.

Geogebraanwendung Steinerellipsen

Eine ähnliche Ellipse, die durch die Mittelpunkte der Seitenmitten geht ist auf folgender Webseite beschrieben:
Matroids Matheplanet Sechs besondere Punkte auf den Seiten eines Dreiecks
Die Ellipse hat den Mittelpunkt und die Achsen mit den Steinerellipsen gemeinsam. Der Flächeninhalt von Inellipse zu dieser Ellipse hat das Verhältnis von 1:7/4.
Eine ähnliche innere Ellipse hat das Verhältnis von 1:16/13.
Die ähnliche äußere Ellipse hat das Verhältnis von 1:43/16.